Definimos el problema canonico de programación lineal como:
- Variables del sistema como un vector x = [x1, x2, …]
- Esta pueden ser variables del sistema, como cantidad de materia prima, etc.
- Funcion costo com una función escalar
- Puede ser la utilidad total a maximizar o el costo a minimizar, etc.
- Ecuaciones de inequaliadad (forma matricial
)
- Restricciones en los recursos, por lo general delimitado por un borde superior ( upper bound)
- Ecuaciones de restricciones de igualdad (forma matricial
)
- Restricciones menos comunes, se impone una igualdad en un sistema lineal .
- Limites para cada variable
. Una lista de tuplas (minimo, máximo) para cada variable.
- Límites para cada variable, por ejemplo x1 no puede ser menos que cero o mayor que 10. Este parametro es opcional y en caso de no especificarlos se asumirá no negatividad y sin limite superior.
La funcion para optimizazar es linprog() y sus parametros son:
scipy.optimize.linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None, bounds=None, method=’interior-point’, callback=None, options=None, x0=None)
Donde:
- c : es el vector de pesos o coeficientes de la funcion costo.
- A_ub: es la matriz de coeficientes para el sistema de restricciones «menos que».
- b_u: es el vector de coeficientes libres en el sistema de ecuaciones.
- A_eq (opcional): es la matriz de coeficientes para el sistema de restricciones «igual que».
- b_eq (opcional):es el vector de coeficientes libres en el sistema de ecuaciones de igualdad.
- bounds(opcional): lista de tuplas(min,max) para cada variable x
- method: cadena de texto del metodo a utilizar y tenemos 3 opciones
- ‘interior-point’ (en defecto)
- ‘revised simplex’ (recomendado)
- ‘simplex’ (obsoleto)
- x0: valores inciciales para inciar el proceso iterativo
Al llamar la funcion linprog() esta retorna un objeto resultado (OptimizedResult). Este objeto tiene como atributos importantes:
- x: resultado
- message: texto o mensaje del solver
Ejemplo
- Un ejemplo clásico es maximizar la utilidad de
- Sujeto a a cuatro restricciones:
- Este ejemplo es tomado del libro: TAHA, HAMDY A. Investigación de operaciones, 7a. edición. PEARSON EDUCACIÓN, México, 2004; ISBN: 970-26-0498-2
Podemos escribir las restricciones de foma matricial ( producto matriz-vector):
Paso 1: funcion costo
Paso2: c = [5.0, 4.0] *Pero la funcion de scipy linprog(…) solo minimiza, tenemos que invertir los signos delos coeficientes de c para maximizar. Por lo tanto c = [-5.0, -4.0]
Paso3: Sabiendo que entonces las matrices
y el vector libre es:
Paso 4: No tenemos restricciones de igualdad.
Paso 5: Como las restricciones son las clasicada de no negatividad podemos dejaar el parametro por defecto «None»
Listo, tenemos las matrices y vectores que defninen el problema de optimizacion lineal ahora vamos presentar un codigo de ejemplo, primero importamos las librerias necesarias:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import linprog
Creamos las variables con las matrices previamente definidas:
c = np.array([-5.0, -4.0]) # Coeficientes de la funcion costo
A = np.array([[6,4],[1,2],[-1,1],[0,1]]) # coeficientes de la matriz de inequalities
b = np.array([24, 6, 1, 2]) # coeficientes libres
Llamamos la funcion linprog de scipy (en el submodulo de optimize):
res = linprog(c, A, b, method="revised simplex")
print(res) # mostramos la estrucutra OptimizedResult
Y podemos observar que el resultado converge:
con: array([], dtype=float64)
fun: -21.0
message: 'Optimization terminated successfully.'
nit: 2
slack: array([0. , 0. , 2.5, 0.5])
status: 0
success: True
x: array([3. , 1.5])
Por Ultimo podemos visualizar la respuesta (dos dimensiones) y creamos una funcion reutilizable que se llame plot_contr(…) y esta recibe las matricez que definene el problema ademas de dos parametros especiales.
El primero es una tupla que nos dicel el limite de la grafica (x_max, y_max). El segundo parametro especial, es una 3-tupla que controla la grafica delas isolineas de la funcion costo (min,max, paso).
def plot_constr(c,A,b,limites,zz):
"""Author Stephen Krol 2020 <stephendata.science.blog>"""
N = A.shape[0]
print("Number of contraints inequalities: ", N)
plt.figure()
plt.title("Cost: z = "+ " + ".join([str(x)+" x"+str(i+1) for i,x in enumerate(c)]))
X = np.linspace(0,15)
for i in range(0,N):
c_txt = " + ".join([str(x)+" x"+str(i+1) for i,x in enumerate(A[i,:])]) + " <= " + str(b[i])
plt.plot(X, -X*(A[i,0]/A[i,1]) + b[i]/A[i,1] ,label = c_txt )
for j in range(zz[0],zz[1], zz[2]):
c_txt = "z = " + str(j)
plt.plot(X, -X*(c[0]/c[1]) + (j/c[1]), "--" ,label = c_txt )
res = linprog(c, A, b, method="revised simplex")
plt.plot(res.x[0],res.x[1],"ro", label="Solucion")
plt.xlim(0,limites[0])
plt.ylim(0,limites[1])
plt.legend()
plt.grid()
plt.show()
Si deseamos saber el valor de la utilidad en la solucion simplemente podemos evaluar la funcion z(x) aplicando el producto vector tranpuesto por vector:
np.dot(res.x.T , -c)
Esto nos devuelve z = 21, que es la solucion optima factible para x1 = 3.0 y x2 = 1.5 .
Podemos graficar las respuestas de 0 a -21 con soluciones de en 5 en 5 de la siguiente manera:
plot_constr(c,A,b,[6,6],[-21,0,5])
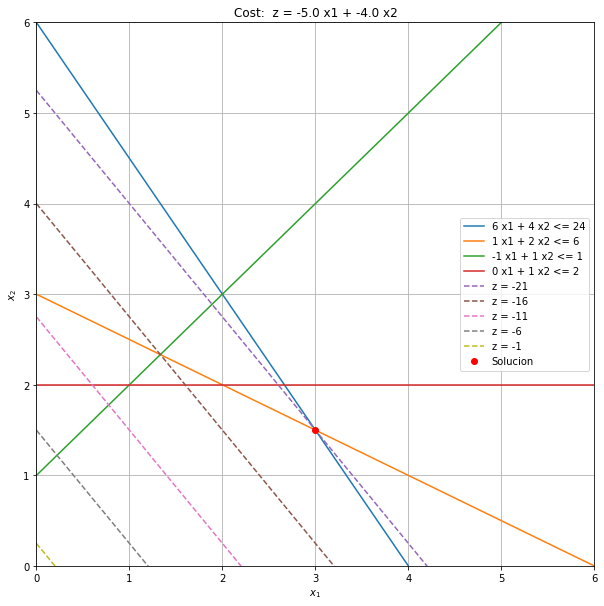
Podemos ver la region factible debajo y acotada por la linea verde, naranja, roja y azul (resctricciones). Las posibles soluciones de z en lineas puntedas.
La combinación optima ocurre en x1= 3.0 y x2= 1.5 con un valor de z=21, cualquier otra solución factible produce un valor de z menor.
Pudes descargar el Jupyter Notebook:
2 replies on “Programación lineal con Python”
Que interesante. Lo explicas muy bien! Saludos desde Alemania
Me gustaLe gusta a 1 persona
Muchas gracias, me ha servido mucho.
Me gustaLe gusta a 1 persona